Pembahasan Soal SBMPTN 2014 TKD SAINTEK Matematika IPA Kode Soal 512
Nomor 1
Agar 1, a2, -2a2√2 dan masing-masing merupakan suku ke 3, suku ke 5, dan suku ke 8 suatu barisan geometri, maka rasio barisan tersebut adalah ....
A. -2
B. -√2
C. 2
D. 2√2
E. 4
Pembahasan :
Perhatikan bahwa tantangan soal disini adalah bagaimana mengeliminasi , sehingga dengan mudah diperoleh rasio barisan geometri tersebut. Hati-hati, disini variabel a tidak melambangkan suku pertama. Oleh karena itu, untuk menghindari kesalahpahaman maka suku pertama pada rumus umum suku ke-n kebarisan geometri kita ganti menjadi huruf ‘a’ besar sebagai berikut:
Un=Arn-1
Perhatikan juga bahwa pada suku ke 5 dan suku ke 8 memuat masing-masing bentuk a2 yang tentunya bisa dieliminasi dengan sebuah perbandingan berikut:
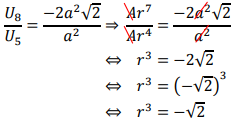
Jadi, rasio barisan tersebut adalah -√2.
Dimana seandainya ditanyakan nilai a, maka dengan mudah nilai a bisa ditemukan dari perbandingan berikut:
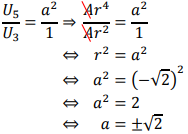
Banyaknya akar real f(t) = t9 - t adalah ....
A. 2
B. 3
C. 4
D. 6
E. 9
Pembahasan :
Perhatikan f(t) = t9 - t.
Mencari banyaknya akar real dari f(t), berarti sama halnya dengan mencari nilai yang menyebabkan f(t) = 0. Banyak akar real tersebut bisa ditentukan dengan mencari berapa jumlah faktor linear dari f(t) dengan cara memfaktorkannya terlebih dahulu sebagai berikut:
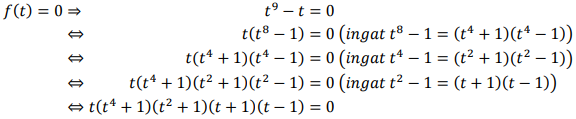
Sehingga ada 3 buah faktor linear yaitu t, (t + 1), dan (t - 1).
Jadi, ada 3 buah akar-akar penyelesaian suku banyak yaitu 0, -1, dan 1.
Jawaban : B
Nomor 3
Nilai a yang menyebabkan persamaan 9x - a . 3x + a = 0 mempunyai tepat satu akar nyata adalah ....
A. 4
B. 0 atau 4
C. a < 0
D. a < 0 atau 4
E. a < 0 atau a > 4
Pembahasan :
Perhatikan,
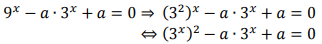
Bentuk persamaan di atas serupa dengan bentuk persamaan kuadrat asalkan kita mau memisalkan bentuk 3x dulu supaya menjadi lebih sederhana.
Misal 3x = p maka persamaan diatas menjadi,
(3x)2 - a . 3x + a → p2 - ap + a = 0
Nah, bentuk p2 - ap + a = 0 akan tepat memiliki satu akar nyata apabila nilai diskriminan persamaan kuadrat tersebut adalah nol.
Pada persamaan kuadrat p2 - ap + a = 0, diperoleh nilai A = 1, B = -a, C = 0
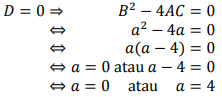
Perhatikan, 3x > 0, maka apabila a = 0 menyebabkan (3x)2 = 0.
Jelas bahwa a = 0 bertentangan dengan syarat 3x > 0.
Jadi, jawaban yang memenuhi hanya a = 4 saja.
Nomor 4
Bila sin x + cos x = a, maka sin4 x + cos4 x ....
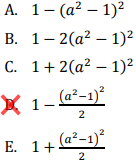
Pembahasan :
Perhatikan, dari bentuk sin x + cos x = a , apabila kita kuadratkan maka akan diperoleh:
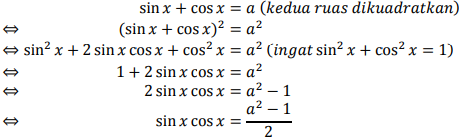
Perhatikan juga bahwa pada soal ditanyakan nilai dari sin4 x + cos4 x yang dapat diperoleh dari:
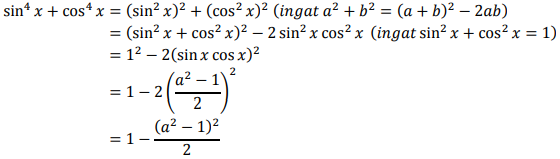
Jawaban : D
Nomor 5
Sebuah toko makanan menyediakan es krim dengan 6 rasa berbeda. Banyak cara seseorang pembeli dapat memilih 5 es krim dengan 3 rasa berbeda adalah ....
A. 6
B. 20
C. 22
D. 40
E. 120
Pembahasan :
Perhatikan, dalam memilih 5 es krim dengan 3 rasa berbeda, ada dua kemungkinan:
- Sudah pasti terpilih 3 rasa berbeda, 2 es krim yang lain memiliki rasa yang sama.
n(A) = 6C3 x 3C1 = 20 x 3 = 60
- Sudah pasti terpilih 3 rasa berbeda, tapi 2 es krim yang lain rasanya berbeda.
n(B) = 6C3 x 3C2 = 20 x 3 = 60
Jadi, total cara seorang pembeli dapat memilih 5 es krim dengan 3 rasa berbeda adalah:
n = n(A) + n(B) = 60 + 60 = 120
Jawaban : E
Nomor 6
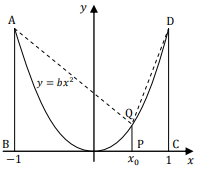
Misalkan A(t) menyatakan luas daerah di bawah kurva y = bx2, 0 ≤ x ≤ t . Jika titik P(x0,0) sehingga A(x0):A(1) = 1:8, maka perbandingan luas trapesium ABPQ:DCPQ ....
 A. 2 : 1
A. 2 : 1
B. 3 : 1
C. 6 : 1
D. 8 : 1
E. 9 : 1
Pembahasan :
Perhatikan, A(t) adalah luas daerah di bawah kurva y = bx2, 0 ≤ x ≤ t.
A(t) dapat dinyatakan dalam integral tertentu sebagai berikut:
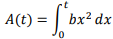
Perhatikan, pada soal diketahui bahwa A(x0) : A(1) = 1 : 8, sehingga diperoleh:
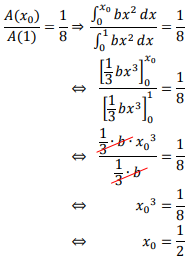
Sehingga, perbandingan luas trapesium ABPQ : DCPQ adalah
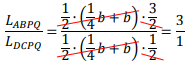
Jawaban : B
Agar 1, a2, -2a2√2 dan masing-masing merupakan suku ke 3, suku ke 5, dan suku ke 8 suatu barisan geometri, maka rasio barisan tersebut adalah ....
A. -2
B. -√2
C. 2
D. 2√2
E. 4
Pembahasan :
Perhatikan bahwa tantangan soal disini adalah bagaimana mengeliminasi , sehingga dengan mudah diperoleh rasio barisan geometri tersebut. Hati-hati, disini variabel a tidak melambangkan suku pertama. Oleh karena itu, untuk menghindari kesalahpahaman maka suku pertama pada rumus umum suku ke-n kebarisan geometri kita ganti menjadi huruf ‘a’ besar sebagai berikut:
Un=Arn-1
Perhatikan juga bahwa pada suku ke 5 dan suku ke 8 memuat masing-masing bentuk a2 yang tentunya bisa dieliminasi dengan sebuah perbandingan berikut:
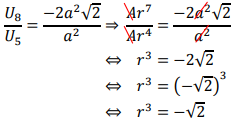
Jadi, rasio barisan tersebut adalah -√2.
Dimana seandainya ditanyakan nilai a, maka dengan mudah nilai a bisa ditemukan dari perbandingan berikut:
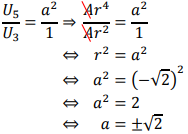
Jawaban : B
Nomor 2
Banyaknya akar real f(t) = t9 - t adalah ....
A. 2
B. 3
C. 4
D. 6
E. 9
Pembahasan :
Perhatikan f(t) = t9 - t.
Mencari banyaknya akar real dari f(t), berarti sama halnya dengan mencari nilai yang menyebabkan f(t) = 0. Banyak akar real tersebut bisa ditentukan dengan mencari berapa jumlah faktor linear dari f(t) dengan cara memfaktorkannya terlebih dahulu sebagai berikut:
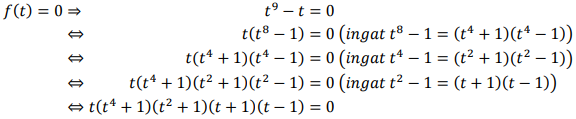
Sehingga ada 3 buah faktor linear yaitu t, (t + 1), dan (t - 1).
Jadi, ada 3 buah akar-akar penyelesaian suku banyak yaitu 0, -1, dan 1.
Jawaban : B
Nomor 3
Nilai a yang menyebabkan persamaan 9x - a . 3x + a = 0 mempunyai tepat satu akar nyata adalah ....
A. 4
B. 0 atau 4
C. a < 0
D. a < 0 atau 4
E. a < 0 atau a > 4
Pembahasan :
Perhatikan,
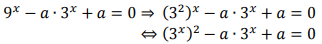
Bentuk persamaan di atas serupa dengan bentuk persamaan kuadrat asalkan kita mau memisalkan bentuk 3x dulu supaya menjadi lebih sederhana.
Misal 3x = p maka persamaan diatas menjadi,
(3x)2 - a . 3x + a → p2 - ap + a = 0
Nah, bentuk p2 - ap + a = 0 akan tepat memiliki satu akar nyata apabila nilai diskriminan persamaan kuadrat tersebut adalah nol.
Pada persamaan kuadrat p2 - ap + a = 0, diperoleh nilai A = 1, B = -a, C = 0
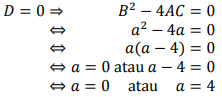
Perhatikan, 3x > 0, maka apabila a = 0 menyebabkan (3x)2 = 0.
Jelas bahwa a = 0 bertentangan dengan syarat 3x > 0.
Jadi, jawaban yang memenuhi hanya a = 4 saja.
Nomor 4
Bila sin x + cos x = a, maka sin4 x + cos4 x ....
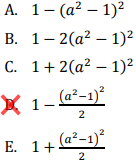
Perhatikan, dari bentuk sin x + cos x = a , apabila kita kuadratkan maka akan diperoleh:
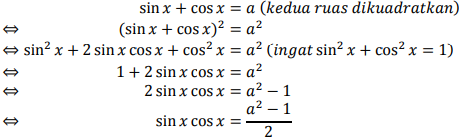
Perhatikan juga bahwa pada soal ditanyakan nilai dari sin4 x + cos4 x yang dapat diperoleh dari:
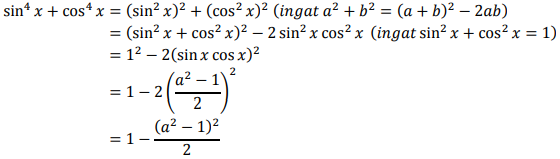
Jawaban : D
Nomor 5
Sebuah toko makanan menyediakan es krim dengan 6 rasa berbeda. Banyak cara seseorang pembeli dapat memilih 5 es krim dengan 3 rasa berbeda adalah ....
A. 6
B. 20
C. 22
D. 40
E. 120
Pembahasan :
Perhatikan, dalam memilih 5 es krim dengan 3 rasa berbeda, ada dua kemungkinan:
- Sudah pasti terpilih 3 rasa berbeda, 2 es krim yang lain memiliki rasa yang sama.
n(A) = 6C3 x 3C1 = 20 x 3 = 60
- Sudah pasti terpilih 3 rasa berbeda, tapi 2 es krim yang lain rasanya berbeda.
n(B) = 6C3 x 3C2 = 20 x 3 = 60
Jadi, total cara seorang pembeli dapat memilih 5 es krim dengan 3 rasa berbeda adalah:
n = n(A) + n(B) = 60 + 60 = 120
Jawaban : E
Nomor 6
Misalkan A(t) menyatakan luas daerah di bawah kurva y = bx2, 0 ≤ x ≤ t . Jika titik P(x0,0) sehingga A(x0):A(1) = 1:8, maka perbandingan luas trapesium ABPQ:DCPQ ....

B. 3 : 1
C. 6 : 1
D. 8 : 1
E. 9 : 1
Pembahasan :
Perhatikan, A(t) adalah luas daerah di bawah kurva y = bx2, 0 ≤ x ≤ t.
A(t) dapat dinyatakan dalam integral tertentu sebagai berikut:
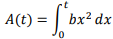
Perhatikan, pada soal diketahui bahwa A(x0) : A(1) = 1 : 8, sehingga diperoleh:
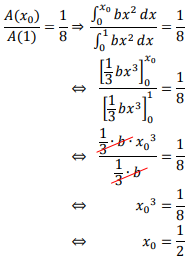
Sehingga, perbandingan luas trapesium ABPQ : DCPQ adalah
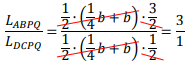
Jawaban : B
0 Komentar untuk "Pembahasan Soal SBMPTN 2014 TKD SAINTEK Matematika IPA Kode Soal 512 "
Post a Comment
Silahkan ditanyakan jika ada yang bingung